In a globalized world, it is no longer enough to consider a bank as though it were isolated from events elsewhere in the financial system. Only by recognizing that the financial market is a complex adaptive system can we begin to tackle areas like risk management, financial crime and disorderly markets. In response to this, banks need simulation models that explicitly capture low-level behavior and the interaction of individual entities within an environment.
What is agent-based modeling?
Agent-based modeling (ABM) is a technique for modeling complex systems to gain a deeper understanding of system behaviors; they simulate how all kinds of people, regulators, corporations, banks, or investors interact with one other and how that interaction could cause specific things to happen to them and to financial markets more broadly.
Agent-based modeling grew out of early work on Cellular Automata, pioneered by John Von Neumann in the 1950s. Cellular Automata (CA) is a discrete model composed of individual “cell-like” entities that perform a range of functions according to a predetermined set of coded instructions.
Conway’s ‘Game of Life’
After the pioneering work of Enrico Fermi in the 1930s, an important contribution to the field was John Conway’s ‘Game of Life’. Though not referred to as an agent-based model at the time of its creation, Conway’s ‘Game of Life’ has become the universal go-to for defining and explaining the concept of an ABM.
The game works like so. Start with a grid of squares. Each square is either filled (alive) or empty (dead)—this is the state of each cell. You can start with any pattern you like.
Each square has eight directly neighboring cells, and each cell updates its state (alive or dead) based on the state of its eight neighbors. Conway designed four update rules:
- Any living cell with fewer than two live neighbors dies, as if dying of isolation.
- Any living cell with two or three live neighbors continues to live.
- Any living cell with more than three live neighbors dies, as if dying of overpopulation.
- Any dead cell with exactly three live neighbors becomes a living cell, as if those cells reproduce.
The game proceeds iteratively—like a turn-based game—and at each turn every cell investigates the neighboring cells and updates according to the rules above.
Extending the analogy to life, we can think of each turn as a generation of the population and the rules are applied repeatedly at each generation—you can see this in Figure 1.
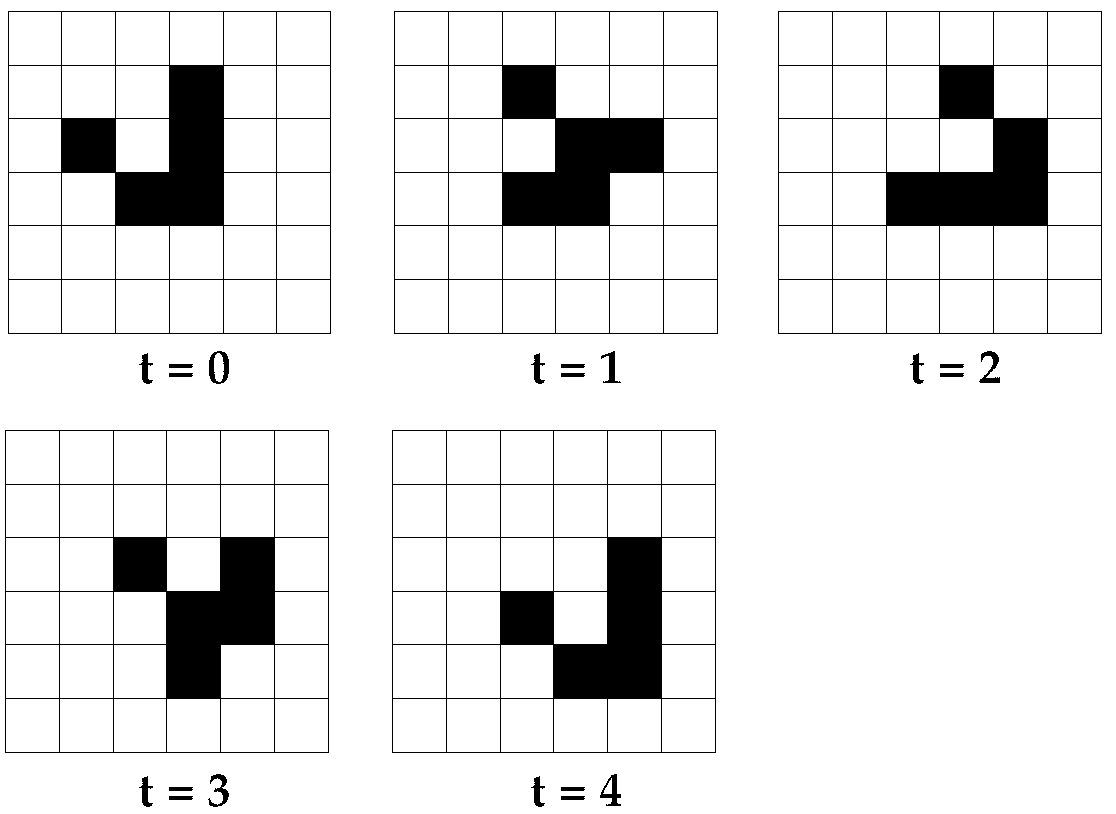
Figure 1: Conway’s Game of Life through time. T = time step.
These simple rules generate complex patterns of movement for the system of cells which seemingly have a life of their own; a life that is far removed from the simplicity of the four rules that govern the cells.
The complex patterns generated by the cells’ interactions are an example of “emergent” properties: properties of the whole system which do not belong to any of its parts.
Interestingly, it’s impossible to know in advance what a starting configuration of the ‘Game of Life’ will generate; the patterns produced are not arbitrary or predictable but are in fact undecidable. The only way to generate them is to compute all the steps—a computational process called simulation.
The simple ideas introduced by CA—stateful entities which update their states based on local information—underpin the much more advanced approach of agent-based modeling.
How do ABMs work?
Agent-based modeling and simulation extends the foundational principles of Conway’s Game of Life.
In agent-based models, the agents are software entities, typically represented computationally as objects. This means that agents themselves hold a state. In Conway’s Game of Life, cells have a very simple state—they are either alive or dead.
In an agent-based model, the state can be any data that describes the agent; for instance, an agent that is used to represent a person could contain information about their age, height and salary.
In Conway’s Game of Life, information from other agents is restricted to just the neighboring eight cells. In an agent-based model, agents can pass information in arbitrarily complex webs of communication. Agents representing people might interact via their social networks which can describe the flow of information between millions of interacting entities. These networks are complex and are formally referred to as graphs. Modeling these graphs is referred to as graph computation.
Why are ABMs so useful?
Banks are starting to realize that ABMs give a more robust view of the financial system and could enhance existing modeling techniques used across their organization. Utilizing these techniques often requires a team of quants with machine learning skills and experience in computational simulation—and this isn’t an insignificant challenge.
Nevertheless, ABMs offer several benefits over traditional modeling techniques which justify the investment. Want to find out more about the benefits? Download the full Guide to ABM for Financial Services below.
